This is a blog series in which I'd like to share my journey/knowledge of programming chess engines so far. I hope to learn/share more in the future, so stay tuned for future posts! Part 1 focuses on implementing a working board/move generation in a low level language such as C/C++.

Background

Chess has always been part of my life, from when I first gained interest in the game at the age of 7. I played in many tournaments throughout my time in primary and secondary school, reaching a peak elo rating of 2319, which would have put me within the top 10 players in Ireland. Here's my lichess page if you want to pop me a message!

Since the start of college, I've entered a "semi-retired" stage, only playing occasional games here and there. This is due to my greater interest in my Computer Science studies, as well as the time, money, and mind consuming nature of the game. However, what greater intersection between my "professional hobby" and my degree than building a chess engine?

Part 1: The Game Representation

If you want to build a complete chess engine end-to-end (highly recommended if you want to really dig into the implementation details!), you start with the game representation itself. This includes all of the logic necessary to generate legal moves, make/unmake moves, and check for game termination. This is much trickier to build from the ground up than it seems! Also, modern engines use all sorts of optimizations to speed up the move generation process that might not be so obvious at first.

Programming Language

Many of the aforementioned optimizations really shine at the lower level of languages, so something on the wavelength of C/C++ is recommended if you want to do it all. However, this may not be accessible to everyone. I used C++ (but really, C), following this excellent video series. If you want to implement in a higher level language like Python or Javascript, also feel free! It's likely you will still learn a lot but will not use some of the lower level concepts such as bit manipulation for move generation. However, I will be sharing what I have learned from the perspective of the lower level programmer, to stay true to my journey.

The Board

There are many possible implementations of representing the chessboard, but the one I learned to implement is a piece-centric one using bitboards. Let me unpack what this entails.

Piece-Centric

A piece-centric representation focuses on which pieces are still on the board for both players. For example, you could maintain an array of white and black pieces, with each entry in the array being a piece object with all of its associated information encoded in the object. However, we don't do this, instead using...

Bitboards!

This is a popular technique where we keep a separate board for each piece type, for each color. In other words, we have a board of only white pawns, only white knights, and so on. There are 6 piece types and 2 colors, so that's 12 bitboards to store the chessboard state. The advantage of this approach is that for each board, we only need to keep track of whether there is/isn't a piece of that type on every square, a Boolean value! So we only require 1 bit/square * 64 = a 64-bit/8-byte word to encode an entire piece-board. Naturally, you should write utility macros/functions to set/unset a piece at a specific location. Constants for the 64 square names help too.

Here's a diagram to illustrate a single bitboard for the white pawns at the start of a game:

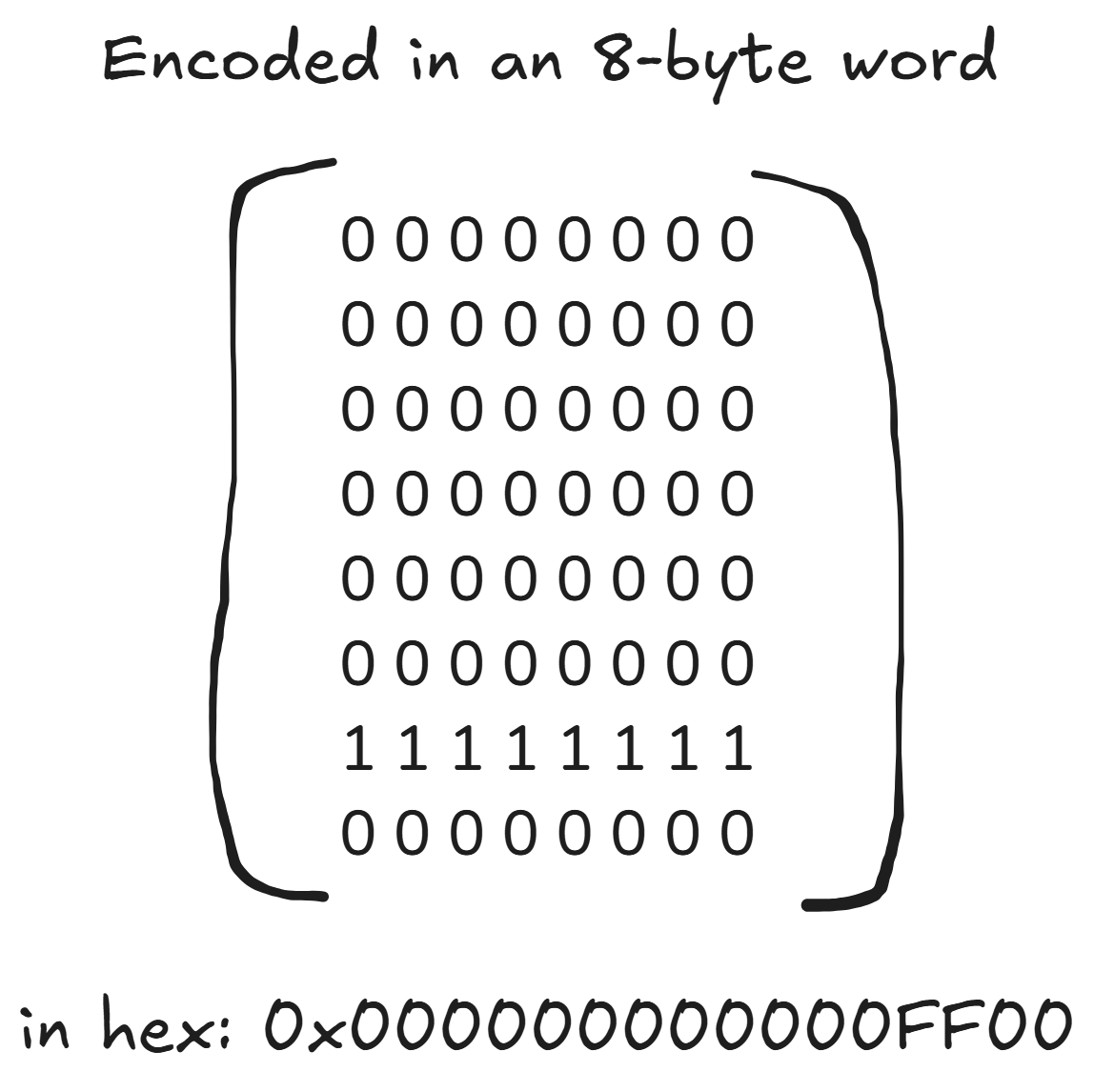
In addition to the bitboards, some extra information is required to capture the full state of a chess game. We need flags for side to move, kingside/queenside castling rights, and en passant square. We also need a counter for non-capture/pawn moves for the 50-move rule, and a way to track repetitions.

Finally, I'll also mention that occupancy bitboards, which keep track of which squares have any white or black pieces, are incredibly useful for the next section. Trust me, you'll need them sooner or later.

With this groundwork in place, we can move on to move generation, the clunkiest part of any chess engine to implement due to its nuances.

Move Generation

So you think move generation is easy? Boy, do I have some news for you... Seriously though, it's so easy to make subtle mistakes in your move generation that don't get spotted until way down the line, at which point you have to go on what feels like a wild goose chase. Chess rules are quite a bit more complicated than a game like Go or Gomoku, so it's important to get this part right. What's nice is that move generation with bitboards is quite elegant! Let me explain with a diagram on how we can generate pawn moves using our pawn bitboard:

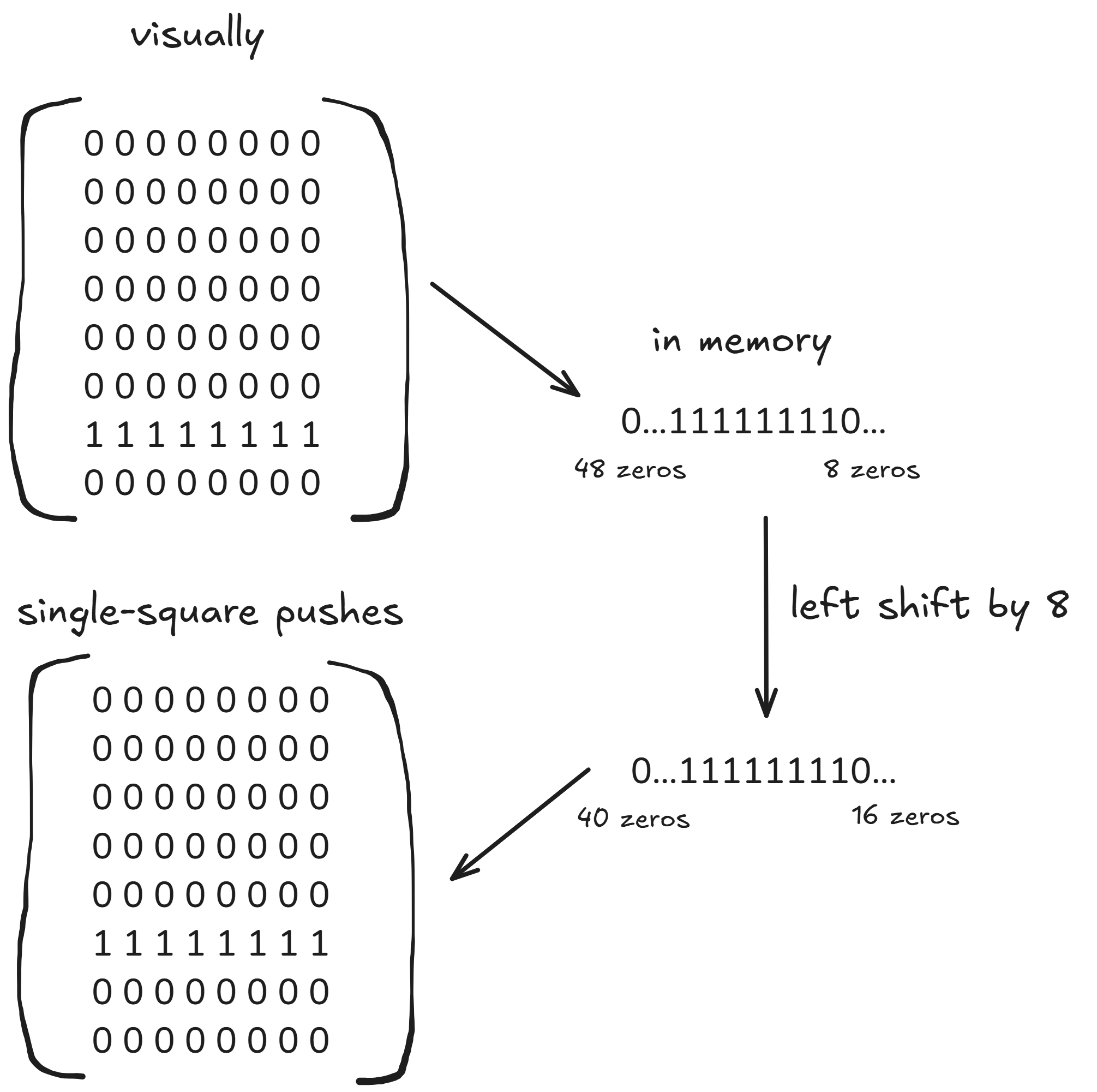
Elegant, right? To do this, we simply take the bitboard for white pawns, and apply a left shift operation by 8 to achieve the resulting bitboard of pushing all pawns forward by 1 square. Now all we have to do is repeatedly get/mask out the LSB to generate the actual moves.

Similar approaches using bit manipulation, bit masking, and adding constants can be used to generate many of the possible move types we require. However, this is the easy part. There are still many nuances to cover, I'll only mention most of them in brief; I'll leave the full implementation up to you to figure out :)

Castling

This one is not as bad as it seems; you just need to be careful with checking/updating the castling flags, and being sure to mask the squares in between the king/rooks to ensure they are not occupied/attacked.

En Passant

Again, easier than it sounds. You only need to keep track of one en passant square each move, since only one pawn could be taken if it moved twice, and only on one square. When generating pawn moves, you just have to take into consideration the current legal square (if any).

Pawn Promotions

There's no getting around this one; you'll just have to do some enumeration to generate all of the possible pawn promotions and pawn capture promotions. It can be easy to miss something here, so tread carefully and be sure to test well.

Sliding Pieces

Rooks, Bishops, and Queens deserve a special note here, as there exists a beautiful technique to generate moves of the sliding sort called Magic Bitboards. The main challenge is that since sliders can be blocked, we can't just perform a simple mask to get all of the legal moves. We have to check in each direction if a friendly/enemy piece is blocking our path, and stop generating moves beyond that point. Additionally, if there is an enemy piece, don't forget to generate that capture.

Pure enumeration of the moves in this way is quite inefficient, so how can we improve?

One idea is to construct a lookup table for each of the 64 squares, where we take the occupancy bitboard of blockers (which remember, is just an 8-byte word), and use it as a key to the table. This table maps to a bitboard of the legal slider moves with that blocker configuration as key. Here's how that might look in practice:

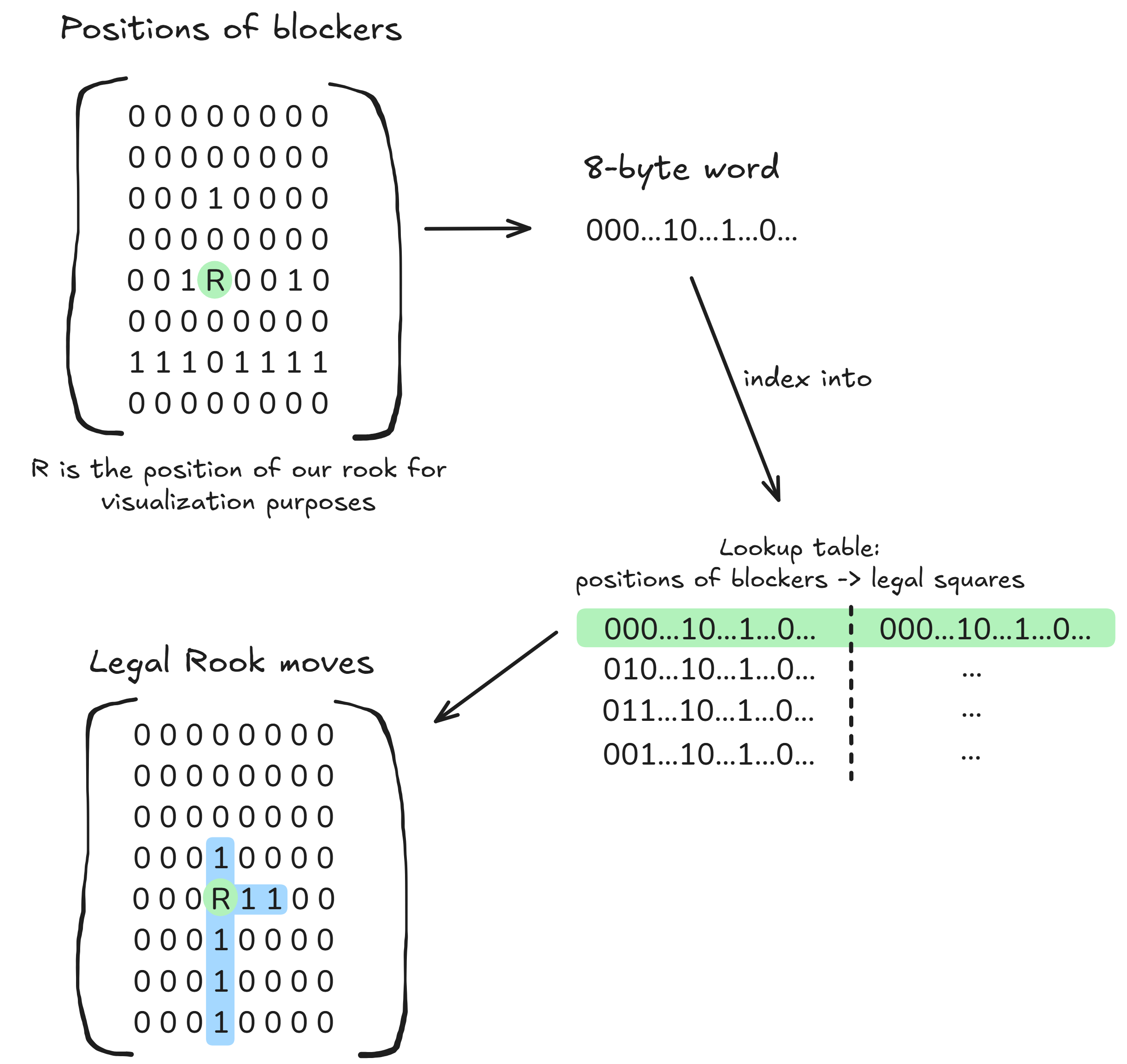
However, can you see the problem? The resulting tables would be huge, since for 63 possible squares of occupancy (excluding the slider square), we would have 2^63 configurations/entries in each lookup table - which needless to say is not a feasible option. Read this classic rice grain story if you're not convinced.

Magic Bitboards

The solution to problem lies in using a perfect hashing algorithm to greatly reduce the size of our lookup table. This is possible because many of the possible blocker configurations map to the same set of legal moves. Therefore, we need a way to transform these equivalent blocker states to the same key for lookup.

What we do is, for each square, compute a "magic number" through brute force. The necessary property of this number is that when we take our occupancy bitboard, multiply it by the number, and mask out a fixed number of bits, we can use the result as an index into a much smaller lookup table of legal moves! Here's an illustration to explain the concept:

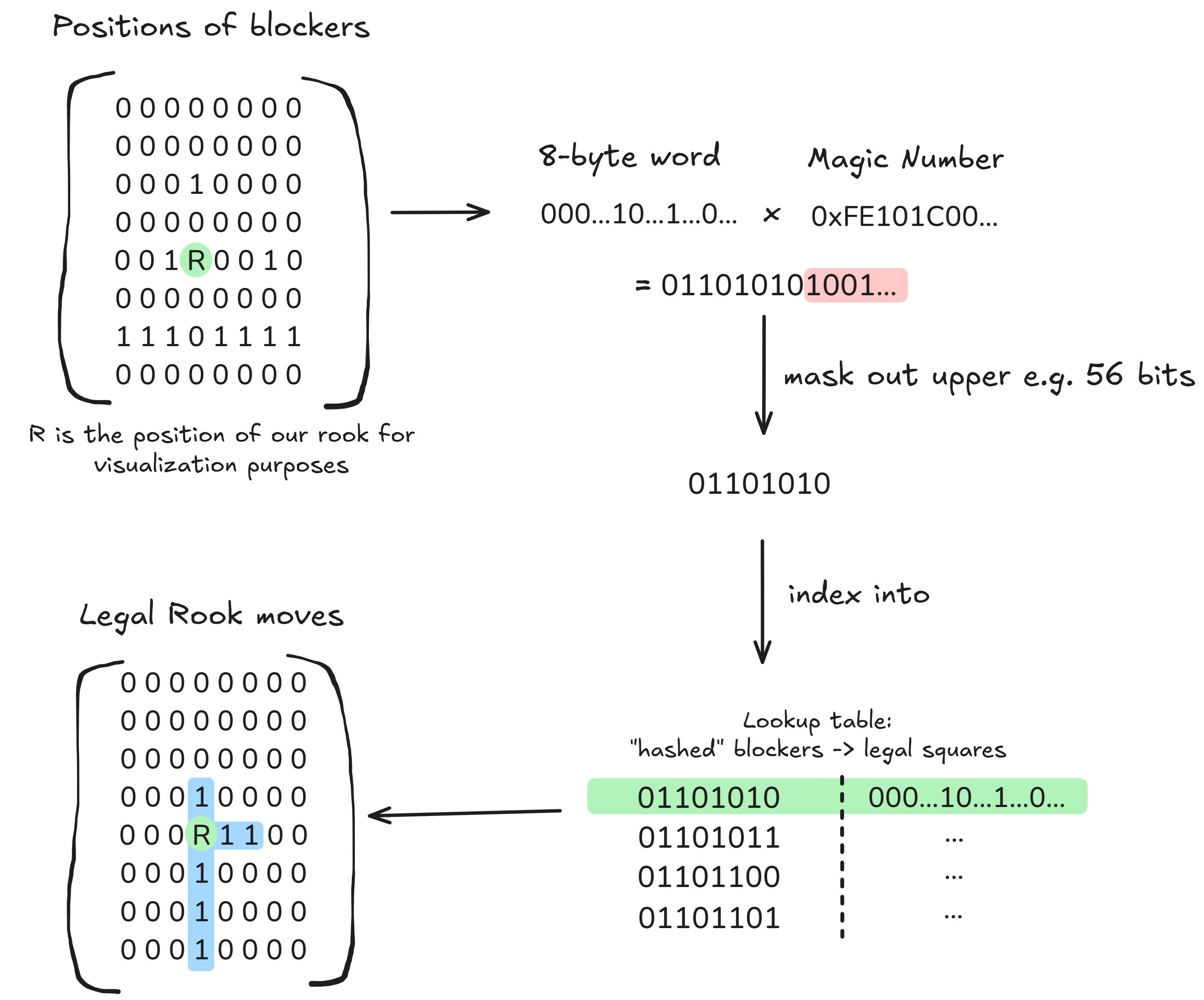
Therefore, we'll have a magic number/reasonably small lookup table per square, for both bishops/rooks. That's 128 numbers/lookup tables to generate, which is computationally feasible. Queen moves can be generated simply by combining both bishop and rook move generations.

A final detail here is that some magic numbers are better than others. The more bits we can mask out to obtain our table key, the smaller the resulting table is going to be. The only way here is to brute force until you find a better/best magic.

Wonderful, isn't it?

And with that, we've described most of the core pieces involved in writing a functional chessboard which generates legal moves in an efficient manner.

Testing

Once you think you have a working chessboard implementation, it's time to test it to see if it actually generates all of the legal moves. A standard way to do this is through Perft tests. Enumerate through all of the legal moves from the starting position up to a certain depth, and keep track of the count. Compare to known values and check to see that they are the same. It's also a good idea to do this for known tricky positions with nuances such as discovered checks, underpromotions and en passants!

Conclusion

Thank you for sticking with me until the end of part 1! I hope you've learned a thing or two about chess engines with me, and stay tuned for part 2 where I'll talk about search algorithms.

Links

• My Github Repository with the C++ engine code
• Chess Programming Wiki is full of amazing resources for engine programming
• Youtube video series by Code Monkey King where I learned much of the methodology